Learning Custom Gestures in Leap Motion

  We had a hack day at the Orchid project in Southampton today. The goal was to incorporate our academic work on home heating into an integrated system. The general idea is to have a computer agent control the thermostat according to your preferences, and to manage things like tariffs in a clever way. We had at our disposal some Rasberry Pi boards for control, but also needed to provide an intuitive user interface to control it. Since I haven't worked at all on home heating, I decided to focus on the interface part, using Leap Motion sensors.

The concept we agreed on involved an animation of a log fire that the home occupant would interact with by gesture (in front of the screen). When the occupant wants to increase the temperature of the house, they can put their hands in front of the fire (visualised on their screen) in the way that people naturally do with campfires (a sort of inverted cupping gesture). When they want to decrease the temperature, they can push the fire away, in a sort of rejection gesture (though of course no-one would do this with a real fire).

The other people in the interface team worked on a nifty animation of a log fire in Javascript, and on communicating with the thermostat. However, Leap does not make it very easy for developers to define custom gestures. It seems that the makers of Leap are trying to establish some standard gestures, which users can learn and use for many apps. Good idea for them, but we wanted more flexibility so I set to work on using machine learning to do online classification of gestures.

My first step was to decide upon a set of features. Downloading the Python developer package. I found a script called Sample.py that prints the data that Leap provides to developers. The most important pieces of data for the two gestures I was interested in were the positions and orientations of the hands (both 3-dimensional).

I wanted the features to be invariant to the absolute position of the hands, so decided on using the speed and orientation of the hands only (4 numbers per time step). Clearly, a more general custom gesture recogniser might use more or different features.

Having decided on the features, I thought more about the machine learning approach to use. The approach needs to take into account the dynamic nature of gestures, i.e., a single gesture may be expressed over multiple time steps. One idea is to assume that the steps of a gesture can be explained by discrete latent states that follow a first-order Markov property. Fortunately, I have just written a package to do variational inference on non-parametric hidden Markov models (HMM) with multi-modal data. The original purpose was for location data (my main area of research), but since I had written it in a fairly re-usable way, only a few lines were required to run inference on the gesture features I defined (4 dimensional continuous feature data):

 K = 20 #truncation parameter for number of components to Dirichlet Process

 mvgSensor = MVGaussianSensor(K,XDim,hyp=obsHyperparams[0])

 exp_z,sensors,exp_a,Zmax = infer(N, [X], K, [mvgSensor], VERBOSE=1,useMix=1, useHMM=1, plotSensor=mvgSensor, plotX=X[:,:2])

In line 1, I set the truncation parameter to a suitably large number of possible components (though the HMM is not required to use all these). Line 2 defines the assumed distribution on the data (a multivariate Gaussian), while line 3 runs the actual inference on the data (X). The assumption is that the logarithm of the velocity, and 3-dimensional orientation of the hands, are normally distributed (and are covariant). Clearly, orientation needs a periodic distribution (as the range of values is between 0 and 2*pi, and values very close to 0 are actually close to 2*pi also), so I would have preferred a von Mises likelihood function there, but there was limited time, so a Gaussian would have to be a good enough approximation. Tthe effects should not be too noticeable, since neither of our gestures involve angles near 0 or 2*pi.

Assuming that the latent states of any user movement (which may include a gesture, or may just be noise), can be inferred correctly, the next step is to include supervision, in order to map the unsupervised inference of movement to known concepts like 'pushing away' or 'hands over fire', (which correspond to 'turn the temperature down!' or 'turn it up!', respectively). Since I hope to have already adequately represented complex movements with the latent states of an HMM, a simple supervised learning approach should be all that is needed. I chose linear least squares regression for this, mostly because it can be done in a single line in NumPy:

 weights = numpy.linalg.lstsq(Z, reshape(Y,(N,1)))

where Z is the set of inferred distributions over latent states and Y is the set of corresponding target values (both for N time steps).

Finally, I created some training data. I spent a few minutes cupping my hands around an imaginary fire, and then another few minutes pushing it away. This gave me a 4000-by-4 feature matrix (with an observation on each row) with which to train. I gave a rough and ready supervision signal (for the final, linear regression step) of 2000 negative outputs ('turn up the heat') followed by 2000 positive outputs ('turn down the heat').

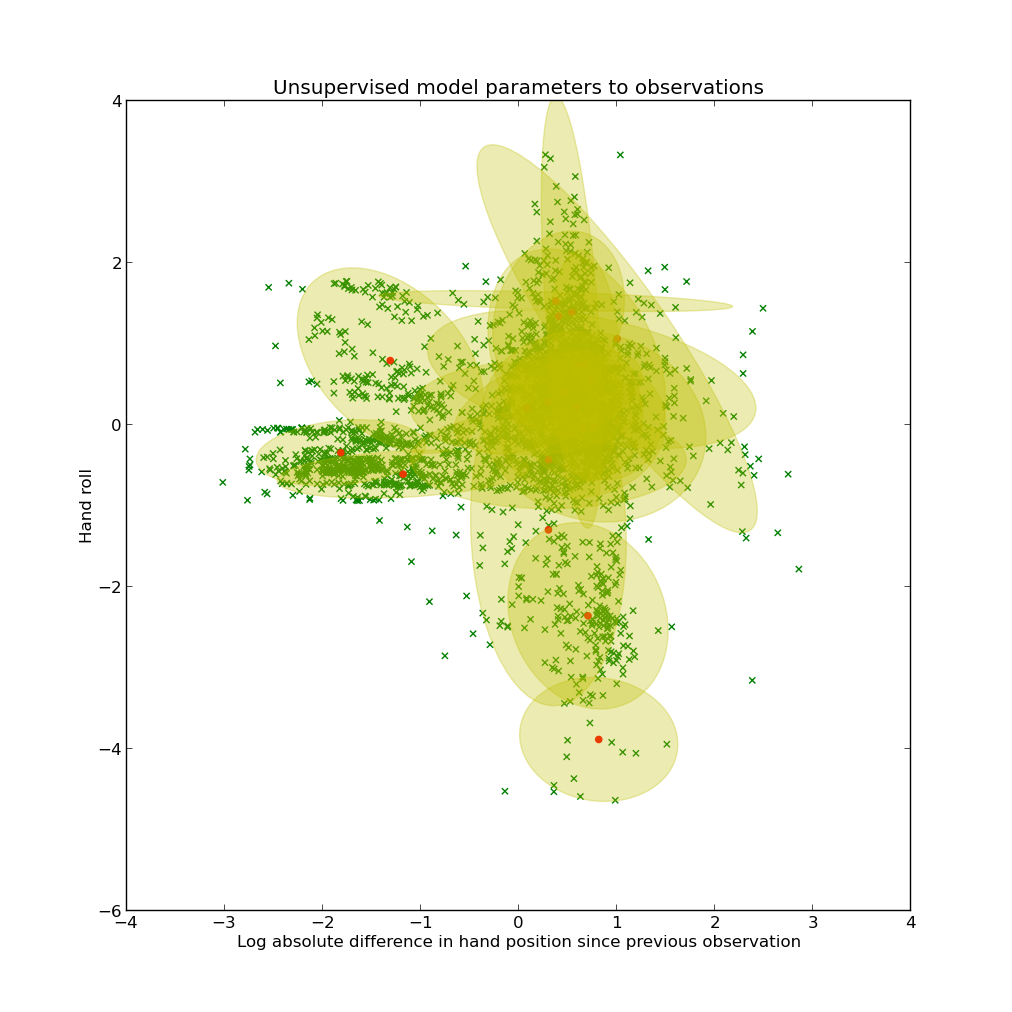
Performing nonparametric HMM inference on this data, the model told me that 19 components were enough to explain the data (which seemed a lot to me):

The graph shows parameters to the Gaussians (mean and covariance) that were learnt to two of the feature dimensions (the other two dimensions are not shown here, but are obviously included in the inference). After applying linear regression, I first tested on the original training data:

In the data I collected, I switched gestures half way through (i.e., a minute or so of me doing the first gesture, and then another minute doing the second gesture). Therefore, one would expect the classification line to be under the threshold at first, then switch to be over the threshold about half way through the data. For comparison, I also plotted how straightforward linear regression (again with least squares, with the green line) does on the raw data (without applying an HMM). We see that simple regression is not enough (achieving 55.6% accuracy), indicating that the raw data is not linearly separable. The combined approach (with the HMM) does much better at 89.8% accuracy.

Of course, this result was from testing with data seen during training, so I then tested on a shorter, unseen data set that I also collected:

My approach achieved 73.8% accuracy (v.s. 53.3% for the simple linear regression). For both data sets, there appears to be portions of the 'hands over fire' gesture (where the expected target value is 0) that spike above the threshold. I think this is because I had to move my hands into place, causing the speed to be non zero. This is important because I think that one important characteristic of the 'hands over fire' gesture is likely to be zero motion. Would be interesting to see how well we do with just the speed feature (without the angles), though I didn't have time for this, and in any case, I've noticed a difference in the angle of my hands between the two gestures.

Overall, I think that kind of accuracy is not bad for a day's work, especially considering that I collected a very small training dataset created in a few minutes of hand waving. I think that if I would collect more data, the results would improve. 73.8% accuracy is probably not good enough yet for this sort of application, as it would obviously be undesirable for the system to turn the thermostat down when the user meant to turn it up (or vice versa). I think the accuracy could be improve a lot with some smoothing, and by somehow dealing with the initial and tail ends of a gesture (which appear to result in a lot of noise). Also, it might be interesting to see how well this works when training on one set of people and testing on another.

In general, I'm excited by the idea of learning a rich representation of behaviour in an unsupervised way, then applying supervision only at the final steps, because it points towards the possibility of collecting a much larger training data set while spending a much smaller amount of time on labelling only some of the data (obviously, this is semi-supervised learning).

I will make all the code I wrote for this available soon.

Here are some additional notes about preprocessing that made a big difference in accuracy for me:

• since the speed feature is non-negative, I took the logarithm of that dimension (resulting in the assumption that the speed is log-normally distributed).
• as per usual, I centred all the data by the mean, and gave it unit standard deviation.